So last time we looked at the corner stone of Quantum Mechanics - Schrodinger equation:
* Note it's a simplified version for 1 dimension.
This time we're gonna look at some simple solutions of this equation, which will show us how microscopic particles behave.
So let's start by simplifying Schrodinger equation for a case of a free moving particle. Since the zero of potential is an arbitrary choice we choose to make U0 = 0. This gives:
 (1)
(1)
Also it is useful for our solution to express the energy E in terms of momentum p (where Ek= (mv^2)/2 & p=mv), which gives:
Substituting (2) into (1) gives:
This can be simplified further using De Broglie's wavelenght (something we covered last time: p=h/lambda) and defining a quantity called wave number k: k= 2pi/lambda:
( Schrodinger equation for a free moving particle)
So how can we solve this equation? We'll it's not a trivial process, and it doesn't really matter for learning the basics, so let's skip to the answer:
(where A is some constant, e is the exponential function, i is the square root of -1 from complex numbers, k is the wave number)
So ok, we solved the SE for a free moving particle and found the wave function, but what does it tell us about the particle? Don't worry we're gonna look at it next time. Thanks for reading!
LINK to lesson 1
LINK to lesson 2
* Note it's a simplified version for 1 dimension.
This time we're gonna look at some simple solutions of this equation, which will show us how microscopic particles behave.
So let's start by simplifying Schrodinger equation for a case of a free moving particle. Since the zero of potential is an arbitrary choice we choose to make U0 = 0. This gives:
 (1)
(1)Also it is useful for our solution to express the energy E in terms of momentum p (where Ek= (mv^2)/2 & p=mv), which gives:
Substituting (2) into (1) gives:
This can be simplified further using De Broglie's wavelenght (something we covered last time: p=h/lambda) and defining a quantity called wave number k: k= 2pi/lambda:
( Schrodinger equation for a free moving particle)
So how can we solve this equation? We'll it's not a trivial process, and it doesn't really matter for learning the basics, so let's skip to the answer:
(where A is some constant, e is the exponential function, i is the square root of -1 from complex numbers, k is the wave number)
Note that this is a time-independent solution. The time dependence of the wave function comes from solving the time dependent Schrodinger equation, which gives:
So ok, we solved the SE for a free moving particle and found the wave function, but what does it tell us about the particle? Don't worry we're gonna look at it next time. Thanks for reading!
LINK to lesson 1
LINK to lesson 2


 5:05 PM
5:05 PM
 silentbob14
silentbob14

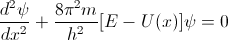





 Posted in:
Posted in: 

0 comments:
Post a Comment