Wonders of Mathematics: Complex Numbers

Everyone, who came across complex numbers in mathematics knows how strange they are. But do these numbers really exist? Are they important?

First let's look at what complex numbers are. More than 2 thousand years ago, ancient Greeks believed that every number can be expressed as a fraction, for example 1/2, 2/5 and so on. However, they were shocked, when they realised that a hypotenuse of a right triangle with sides of length 1 cannot be expressed using natural numbers or fractions. As we all know, the length of the hypotenuse of such a triangle is a square root of 2 (which is 1.414...). This showed ancient Greeks that there is more than a single number system, in this case it's the real number system (which includes counting numbers as 1, 2...., negative numbers, fractions, square roots and so on).

Source

Until complex numbers were found and were used in mathematics, it was thought that all the number systems were already found. So what is a complex number? It's easy. It's a number that is a square root of a negative number.

But do such numbers have any physical meaning? After all, even when calculating simple quadratic equations, younger students are told to ignore negative answers, as negative areas do not exist. Surely such negative areas might not exist, but complex numbers constantly show up in various applications, which shows that even though we can't visualise a square root of -1, it still exists in mysterious ways.

The strange thing about complex numbers in fact is that they almost seem to be existing and not existing at the same time. For example, when solving differential equations, in electrical engineering (also in many other fields), the behaviour of electrical circuits depends on whether the solutions are real or complex numbers.

Another example is quantum mechanics. The wave function, that describes behaviour of microscopic particles is found using complex numbers. That is something real and physical is described by laws which use complex numbers.

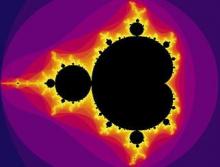
The so called Mandelbrot Set shows a set of complex numbers generated by a simple equation:

Source

Some physics theories even use complex number plane to represent time, whereas real numbers represent spatial dimensions.

But the real question is whether complex numbers represent something physical. When it comes to square roots of positive numbers, we can clearly visualise what they mean. For example, if we know an area of a rectangle is 16 meters, we can take the square root of this number and find out that the side of the rectangle is 4 meters. But when it comes to complex numbers, a similar situation cannot be found.

Posted in: article,complex numbers,ice cold science,mathematics,wonders of mathematics