3x3 Magic Square

Last time we looked at magic squares in general and found out that the most simple magic square is of order 3x3.

There is beautiful legend about the discovery of this popular magic square.

As the story goes, in ancient China there was a huge deluge: the people offered sacrifices to the god of one of the flooding rivers, the Lo river (洛水), to try to calm his anger. A magical turtle emerged from the water with the curious and decidedly unnatural (for a turtle shell) Lo Shu pattern on its shell, which contained the numbers in an aray of a magic square. As the legend says, these numbers showed the people how often and how many sacrificies should be given to calm the Lo river.

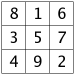
The Lo Shu square containing the numbers on the turtle's back:

 

Image Credit

So what are these magic numbers?

It appears that all magic squares obey some rules. For instance all normal magic squares of un-even order (of  n x n order, where n = 3,5,7...) have a special number at the centre called the magic constant.

So for a 3x3 magic square you have 1+2+3+4+5+6+7+8+9=45. In a magic square you have to add 3 numbers again and again. Therefore the average sum of three numbers is 45:3=15. The number 15 is called the magic number of the 3x3 square.

You can also achieve 15, if you add the middle number 5 three times.  You can reduce 15 in a sum of three sums eight times: 15= 1+5+9;  15= 2+4+9;  15= 2+6+7;  15= 3+5+7
15=1+6+8;  15=2+5+8;  15=3+4+8 ; 15=4+5+6

The odd numbers 1,3,7, and 9 occur twice in the reductions, the even numbers 2,4,6,8 three times and the number 5 four times. Therefore you have to place number 5 in the middle of the magic 3x3 square.

The remaining odd numbers have to be in the middles of a side and the even numbers at the corners. 

*The formula to find other magic constants is:

M= [n(n^2 +1)]/2

So by using the information above we can see that there exists only 1 magic 3x3 square (of numbers 1-9). Of course you can rotate the magic square in total of 8 ways, which gives all the possible distributions of the numbers in a 3x3 magic square.

Thanks for reading!

Read more »

Wonders Of Mathematics - Magic Squares

So one of the books that I really enjoyed recently is the famous Dan Brown's "The Lost Symbol". If you read the book (and you should) you might have noticed that it has many interesting maths references. One of which is hidden in the famous Albrecht Dürer's 1514 engraving Melencolia. It's a very special magic square.

But what are these magic squares? Magic squares are very interesting square arrangements of numbers. The numbers are arranged in such a way, that the sum of all columns, rows and diagonals is equal to the same number.

Magic squares come in different sizes that are called orders, for instance 3x3, 4x4 and so on (it's just a number of rows and columns). As for the sum that is constant for columns, rows and diagonals it's called the magic constant.

 

 

Image Source

The most simple magic square is of order 3x3 (it's easy to see that 2x2 squares are not possible). But how do you construct such a magic square, without relying to guess work? There are various rules, which can help you construct the square faster, however some guess work is still essential.

So when stumbled across these magic squares, I decide it would be fun to found a 3x3 magic square without any help. It's quite fun, well at least much more fun than sudoku, so I encourage you to try it.

Thanks for reading. Next time we're gonna look at all possible 3x3 magic squares and at the mysterious Melancolia engraving.

Read more »